Риски: без их расчета на фондовом рынке никуда. В предыдущих статьях мы разбирали стандартное отклонение и дисперсию (в статье волатильность), как меру риска, сегодня поговорим о коэффициенте бета.
_________________________________________________________

СОДЕРЖАНИЕ СТАТЬИ:
2. Формула беты и ее возможные значения
4. Бета портфеля, бета - нейтральный портфель
5. Где искать уже готовые значения беты
6. Недостатки использования бетты
_________________________________________________________
Коэффициент бета β – показатель ценной бумаги (портфеля), который рассчитывается как мера рыночного риска и дает оценку относительного изменения доходности ценной бумаги (портфеля) по сравнению с доходностью рынка в целом. Проще говоря, этот коэффициент показывает, как рынок воздействует на ценную бумагу.
Коэффициент бета необходим для:
- определения рыночного риска актива (портфеля) относительно рынка в целом;
- составление портфеля, нейтрального к риску;
- расчета оценки стоимости капитала.
Формула беты и ее возможные значения
Общепринятый подход к оценке параметра «бета акции» основывается на регрессионном анализе доходности акции относительно доходности фондового индекса.
Классическая бета или, как ее еще называют «сырая», необработанная бета (raw beta):
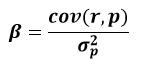
Где:
β – коэффициент бета;
cov (r, p) – ковариация ценной бумаги и портфеля (вместо портфеля часто применяют рыночный индекс, например, индекс Московской Биржи и индекс РТС);
r – доходность актива (ценной бумаги);
p – доходность портфеля (фондового индекса);
σp2– дисперсия портфеля (фондового индекса).
Значения, которые может принимать бета:
β = 1 – доходность такой бумаги будет изменяться одинаково с доходностью рынка (фондового индекса);
β > 1 – доходность (а также изменчивость) таких бумаг очень чувствительна к изменению рынка. Такие активы больше подвержены риску, но потенциально более доходны. В целом, такие ценные бумаги можно назвать агрессивными;
0 < β < 1 – при такой бете активы менее подвержены рыночному риску, как следствие, менее изменчивы. Такие бумаги имеют меньший риск, но и менее доходны в будущем;
β = 0 – отсутствует связь между бумагой и рынком (индексом) в целом;
β < 0 – доходность бумаг, у которых отрицательная бета, идут в противоположные стороны с рынком.
Расчет беты обычным способом и в Excel, а также графическое представление беты на графике
Считать бету будем по следующей формуле: (более развернута, чем формула, приведенная ранее).
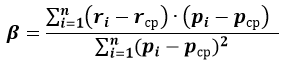
Где:
β – коэффициент бета;
ri – доходность актива в i-ый момент времени;
pi – доходность портфеля (индекса) в i-ый момент времени;
rср – доходность актива в i-ый момент времени;
рср – доходность портфеля (индекса) в i-ый момент времени;
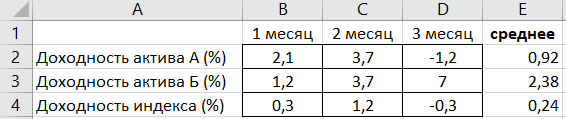
Пример для расчета беты

Совершим расчет беты для актива А
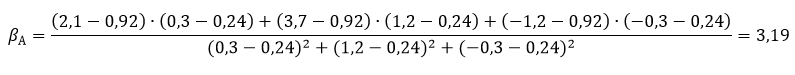
Тот же пример, но с расчетом в Excel
- с помощью опции вставить функцию:
А именно, =ИНДЕКС(ЛИНЕЙН(B2:D2;B4:D4);1) = 3,14
=ИНДЕКС(ЛИНЕЙН(B3:D3;B4:D4);1) = -1,8
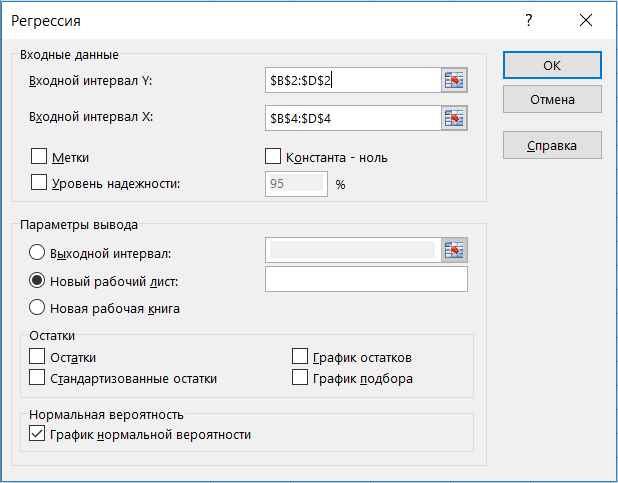
- с помощью пакета «анализ данных» в Excel (пример только для актива А):
Сначала нужно проверить наличие пакета «анализ данных», если не стоит, то установить в файл → параметры → надстройки. Затем в пакете выбираем опцию регрессия и делаем следующие манипуляции, согласно фото
Получаем следующие значения:
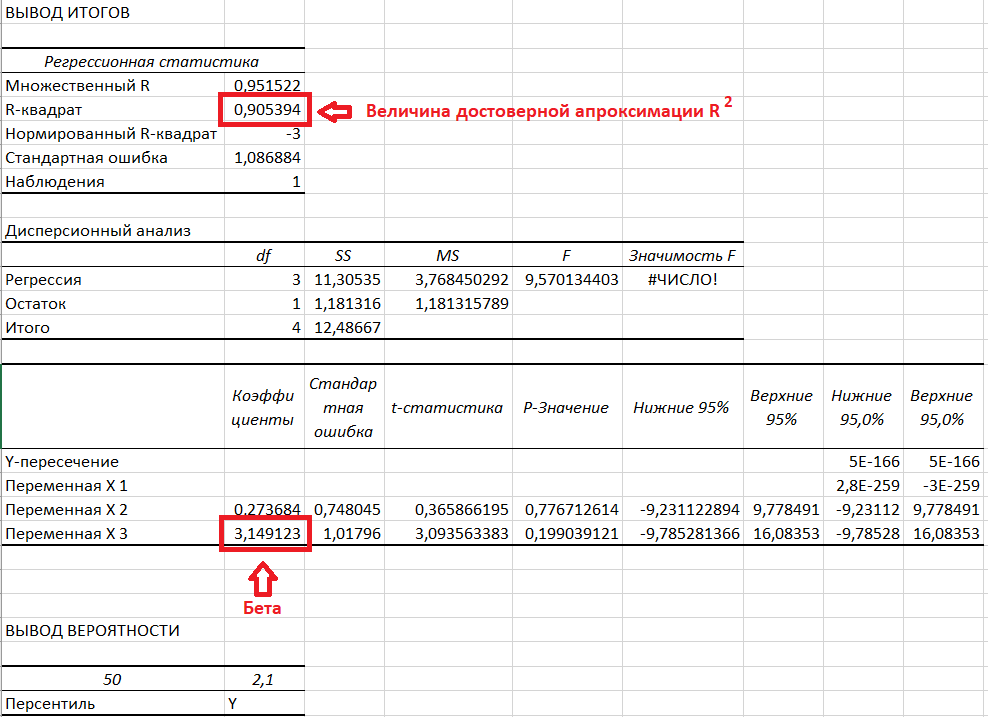
Как видим значения сошлись.
Теперь с помощью Excel покажем графическое представление бета:
На основании данных, приведенных в таблице значений по месяцам построим точечный график зависимости доходности актива А от фондового индекса (в примере будем делать только для актива А)
По оси Х следует вводить значения доходности индекса, по Y - значения доходностей актива.
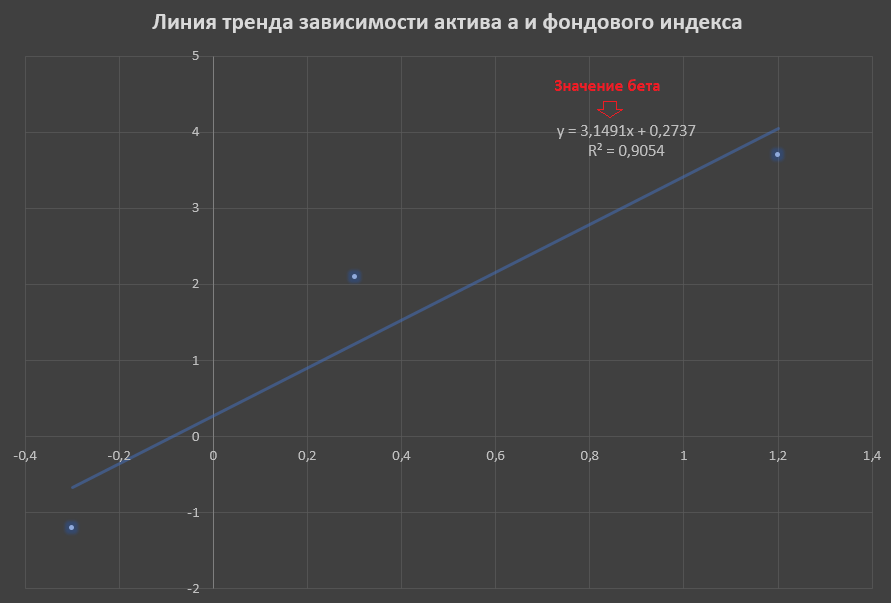
Уравнение тренда – это и есть уравнение линейной регрессии, в котором значение 3,1491 - значение бета. Таким образом можно сказать, что бета представляет собой наклон линии тренда. Значение беты показывает, что при повышении фондового индекса на 1, значение актива возрастает на 3,1491.
Бета портфеля, бета – нейтральный портфель.
Бета портфеля показывает совокупный риск вашего собственного портфеля относительно рынка. Важно понимать, как его рассчитать, чтобы составить портфель максимально нетерпимый к риску, а точнее, независимый от рынка.
Формула расчета беты портфеля:
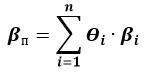
Где:
βп – коэффициент бета портфеля;
Θi– вес i-ого актива в портфеле;
βi – бета i-ого актива в портфеле.
Рассчитаем бету портфеля, в активе которого есть актив А и Б
Возьмем данные из предыдущего примера, для расчетов примем вес актива А в портфеле 10%, актива Б - 90%.
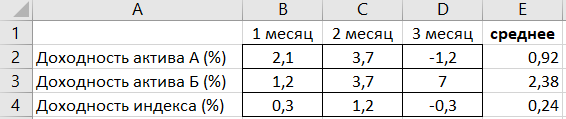
=ИНДЕКС(ЛИНЕЙН(B2:D2;B4:D4);1) = 3,14
=ИНДЕКС(ЛИНЕЙН(B3:D3;B4:D4);1) = -1,8
Значение беты портфеля βп = 3,14·0,1-1,8·0,9 = -1,306
Бета - нейтральный портфель и принципы его составления
Бета-нейтральный портфель, это частный случай, при котором бета портфеля равна нулю
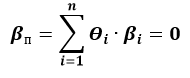
Как же его получить?
- способ №1:
Надо включить в портфель в дополнение к бумагам с положительной бетой, бумаги с отрицательной бетой и с такими весами, чтобы при подсчете беты портфеля она получилась равной нулю.
На практике достаточно мало портфелей имеют бету меньше нуля, но практически к ним можно отнести акции золотодобывающих компаний, т.к. в период кризисов они не просто не падают, а показывают существенный рост. (В России – это акций ПАО «Полюс» и ПАО «полиметалл»).
- способ №2:
Включить в портфель активы, которые не куплены, а проданы (а точнее, в шорте). Т.к. актив в шорте, то перед бетой надо поставить знак -1.
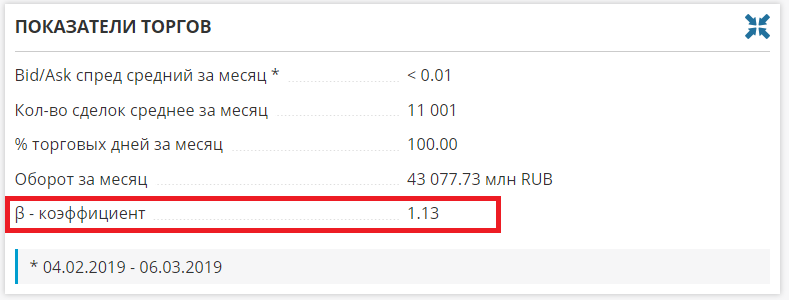
Если нет желания считать бету самостоятельно, то посмотреть ее можно здесь:
Бету всегда можно найти на сайте Московской Биржи, по ссылке:

На сайте investfunds.ru
Недостатки использования беты и их модификации
Как и у любой модели, у методики применения беты есть свои преимущества и недостатки. Многие эксперты пришли к выводу, что для любой акции ее бета не является устойчивым во времени показателем и поэтому не может служить точной оценкой будущего риска.
Для российского рынка характерны следующие недостатки применения модели классической беты:
1) Низкий показатель детерминации. Показывает долю риска, который присущ рыночному риску;
2) Мало информативные значения беты (которые нельзя применять) для акций малой ликвидности и капитализации;
3) Не применим к бумагам, у которых нету исторических цен (на длительном отрезке времени);
4) Коэффициент бета не может предусмотреть реальных положений дел в компаниях.
По всем этим причинам, описанным выше, были выведены модифицированные беты:
Наиболее популярные модификации представлены ниже (2 формулы)
Бета согласно Маршалу Блюму
Его расчеты показали, что со временем величина бета-портфеля приближается к единице, а внутренний риск компании стремится к среднеотраслевому или среднерыночному. Такую бету используют многие инвестиционные банки мира.
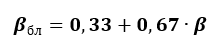
Где:
βбл – бета по Маршалу Блюму;
β – коэффициент классической, сырой беты;
Бета согласно Шоулза-Виллимса
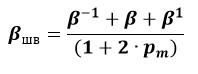
Где:
βшв – бета по Маршалу Блюму;
- коэффициенты бета для предыдущего, текущего и последующего периода;
- коэффициент автокорреляции рыночной доходности.
Удачных Вам инвестиций…!!!
Статьи по теме:
1. Международный валютный фонд (МВФ);
2. Индивидуальный инвестиционный счет (ИИС);
4. Куда инвестировать деньги? (Депозит или Фондовый рынок).